支持向量机

这篇博客主要介绍如何推导svm算法。写这篇博客主要是最近在学习svm算法，想着合上书，自己推导一遍算法的原理，发现还是有很多需要思考的地方。
其实一般推导机器学习算法，是有一个模式的。

定义模型，这里模型理解为如何定义公式
选择损失函数
采用优化算法求损失函数的最小值
推导完毕

比如拿逻辑回归算法举例：

定义模型，即选取sigmoid函数
定义损失函数
采用最大梯度下降算法求损失函数的最小值
得到算法的w和b

但是svm的推导基本上没有怎么提损失函数的内容，大家等会可以在这篇博客中看到如何推导svm算法

判别函数

$h_{w,b}(x) = g(w^T + b)$

上式是SVM的判别函数，其中函数g如下所示：

$g(z)=\left\{ \begin{array}{rcl} 1 & & {z \geq 0 }\\ -1 & & {z < 0 } \end{array} \right.$

即$g(z)$的输出为1时，判别为正例；输出为-1时，判别为反例。

函数间隔和几何间隔(Functional and geometric margins)

函数间隔

对于某一个训练样本$(x^(i), y^(i))$定义函数间隔如下式：

$\hat{\gamma}^{(i)} = y^{(i)}(w^T + b)$

分析函数间隔公式,可以得出如下的结论.当$y^{(i)}=1$时,则$w^T+b>0$,所以$g(z) = 1$;当$y^{(i)}=-1$时,则$w^T+b<0$,所以$g(z) = -1$.所以函数间隔对于判别样本的类别是有作用的.
但是,当我们将$w,b$扩大两倍时,函数函数间隔扩大两倍,但是对于$g(z)$并没有什么变化.即下式成立

$g(2w^T+2b) = g(w^T+b)$

所以更大的函数间隔并不一定比小的函数间隔的置信度大.由此引出了几何间隔

几何间隔

针对几何间隔,我们考虑二维平面,如下图所示: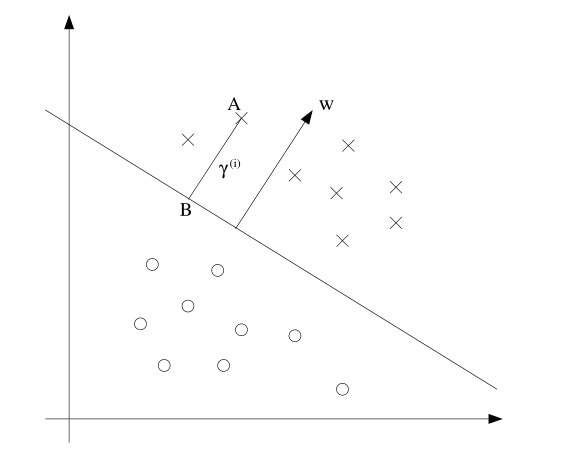

图中的斜线是对应于参数$(w,b)$的决策分隔线.注意$w$是垂直于决策线的,即$w$是决策线的法向量.

证明如下:
设$x_0,x_1$是直线$w^T+b=0$上不同的两个点,则有下式成立
$\left\{ \begin{array}{rcl} w^Tx_0 + b = 0 & & \\ w^Tx_1 + b = 0 & & \end{array} \right.$
两式相减的$w^T(x_0 - x_1) = 0$,而其中$x_0 - x_1$是直线$w^T+b=0$的方向向量,所以w是法向量.

图中$\gamma^{(i)}$是A点对应的几何间隔.设A点为$x^{(i)}$,而向量$w/{\left|w\right|}$是法向量上的单位向量.因此得到B点为$x^{(i)} - \gamma^{(i)}\cdot w/{\left|w\right|}$,又因为B点在分离平面上,所以下式成立:

$w^T(x^{(i)} - \gamma^{(i)}{\frac w {\left\|w\right\|}}) = 0$

从而得到下式:

$\gamma^{(i)} = {\frac {w^Tx^{(i)}+b} {\left\|w\right\|} }=({\frac w {\left\|w\right\|}})^Tx^{(i)} + {\frac b {\left\|w\right\|} }$

如果A点在B点的另外一侧,则B点可以表示为下式:

$x^{(i)} + \gamma^{(i)}\cdot w/{\left\|w\right\|}$$,带入分离超平面,得到几何间隔如下: $$\gamma^{(i)} = -{\frac {w^Tx^{(i)}+b} {\left\|w\right\|} }$

综合两种情况,得到

$\gamma^{(i)} =y^{(i)}(({\frac w {\left\|w\right\|}})^Tx^{(i)} + {\frac b {\left\|w\right\|} })$

具体的公式推导过程中,并没有完全限制在二维平面上(虽然开始展示的图像是二维平面上的),所以对于高维平面也是得到上述公式.
几何间隔反应了样本到分离面的距离,直观上最小的几何间隔越大越好.并且几何间隔中的参数$w,b$可以随意的进行尺度变换而不影响几何间隔的大小(这是因为几何间隔的式子中除以了w的二范数).同时当$\left|w\right|=1$时,几何间隔就等于函数间隔.
定义

$\hat{\gamma} = \min_{i=1,...,m}{\hat{\gamma}^{(i)}}$ ${\gamma} = \min_{i=1,...,m}{\gamma}^{(i)}$

即$\hat{\gamma}$和${\gamma}$分别是函数间隔和几何间隔的最小值.

最优间隔分类器

通过上面的函数间隔和几何间隔,我们自然能够想到优化目标如下式所示:

$\max_{\gamma,w,b} {\gamma} \\ s.t.\quad y^{(i)}(w^T + b) \geq \gamma, i=1,...,m \\ \left\|w\right\|=1 \tag{1.1}$

即在满足所有样本的几何间隔都大于最小几何间隔的情况下,求使得几何间隔最大的参数$w,b$
我们可以将上述优化公式转变成用函数间隔进行表达,如下式所示:

$\max_{\gamma,w,b} {\frac {\hat\gamma} {\left\|w\right\|}}\\ s.t.\quad y^{(i)}(w^T + b) \geq \hat\gamma, i=1,...,m \tag{1.2}$

上述两个优化问题为什么等价?因为$\gamma={\frac {\hat\gamma} {\left|w\right|}}$.针对优化公式(1.2),即求取几何间隔最大,同时在约束不等式两边同时除以$\left|w\right|$,即得所有的几何间隔都大于最小的几何间隔.这即等价于优化公式(1.1)

由于参数$w,b$进行尺度变化,所以我们可以固定函数间隔等于1,即$\hat\gamma=1$
最终将优化公式化简为下式:

$\min_{\gamma,w,b}{\frac 1 2}{\left\|w\right\|}^2 \\ s.t.\quad y^{(i)}(w^T + b) \geq 1, i=1,...,m \tag{1.3}$

针对这个优化公式,即满足不等式的条件下,求取二次函数的最小值,虽然可以采用优化算法求取此最优值.但是我们下面介绍拉格朗日对偶来进行求取,第一求取最优值会变得更加简单,第二能够使用核函数.

拉格朗日对偶(Lagrange duality)

拉格朗日对偶主要是将优化公式转变为其对偶形式,具体的推导过程可以参考Andrew Ng cs229课程中的内容.

再次求解最优间隔分类器

通过拉格朗日对偶,将SVM的优化目标转变为对偶形式,从而得到参数$w,b$