这是一篇翻译文章,但是也不全是,主要是读了文章之后,用自己的话将其复述出来
来源: CS231n Convolutional Neural Networks for Visual Recognition
CNN
卷积神经网络跟一般的神经网络是非常相似的.它们都由神经元组成,并且这些神经元上都有需要学习的权重和偏置项.每个神经元接收输入,执行点积,然后可选择的将输出进行非线性运算.整个网络表示了一个可微的得分函数:即从原始的图像像素到对应的类.两者都有一个损失函数(例如:SVM/Softmax),并且在一般神经网络中用到的技术也能应用到CNN中.
两者的区别在哪里呢?ConvNet网络假设输入是图像,所以我们能够将某些属性编码到网络结构中.这使得前馈函数更有效率并且能极大的减少网络中的参数.
CNN结构概览
回顾:在一般的神经网络中,神经网络接收一个输入(一个向量),然后经过一系列的隐藏层进行转换.每个隐藏层是由一组神经元组成,每个神经元都与前一层的所有神经元相连,属于同一层的神经元完全独立并且不共享任何连接.最后一层是输出层,在分类问题中,它代表了类的得分.
一般的神经网络不能很好的扩展到完整的图像.在CIFAR-10中,一副图像的大小是32$\times$32$\times$3,所以隐藏层中的一个神经元上将会有32$\times$32$\times$3=3072个权重.参数的数量仍然可以接受,但是全连接结构不能扩展到更大的图像上了.例如,如果图像的大小为200$\times$200$\times$3,那么一个神经元将需要200$\times$200$\times$3=120000个权重.可见,全连接神经网络需要的参数将会非常多.这会导致过拟合.
卷积神经网络充分利用了输入是图像的事实,并且用一个更加合理的方式约束了神经网络的结构.特别的,与一般的神经网络不同,卷积神经网络各层由三维排列的神经元组成:宽度,高度,深度(注意,这里的深度指的是激活的第三维,而不是整个神经网络的深度).例如,在CIFAR-10中的输入图像的维度是32$\times$32$\times$3.我们很快会看到,当前层的神经元仅仅连接前一层中的部分神经元.此外,对于CIFAR-10最终的输出层的维度是1$\times$1$\times$10,因为ConvNet最后会将整个图像转换为一个类得分向量,下面是可视化:
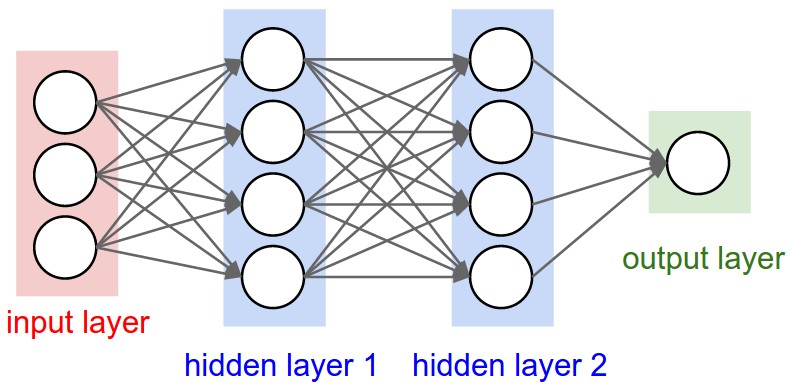
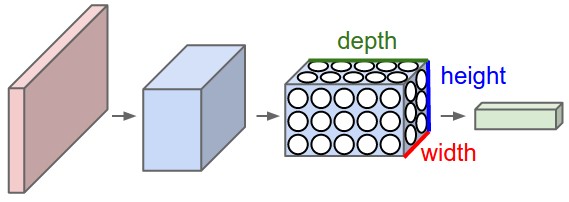
上图表示一个三层的神经网络,下图表示卷积神经网络.
A ConvNet is made up of Layers. Every Layer has a simple API: It transforms an input 3D volume to an output 3D volume with some differentiable function that may or may not have parameters.
ConvNet 层
就像我们上面描述的,一个简单的ConvNet是一系列层组成,ConvNet的每层通过一个可微的函数将输入转化到输出.ConvNet主要由卷积层,池化层和全连接层组成.下面是一个针对CIFAR-10的简单例子:
- INPUT(32$\times$32$\times$3):输入是原始图像的像素,一副图像的宽是32,长是32,并且有三个颜色通道R,G,B
- 卷积层:当前层的神经元只连接前一层的部分神经元.如果我们使用12个过滤器,则经过卷积层后的维度是[32$\times$32$\times$12]
- RELU:对于输入采用ReLu激活函数,并不会改变输入维度,如果前一个维度是[32$\times$32$\times$12],则经过ReLu之后仍然是[32$\times$32$\times$12]
- POOL:池化层会在空间维度上执行下采样,这会导致维度变化,[16$\times$16$\times$12],但是注意最后一维没有改变
FC(全连接层):这是一个全连接的结构,最后的输出是[1$\times$1$\times$10].
卷积神经网络就是将原始的像素图像经过一层一层的计算,最后得到最终的分类得分.注意有些层需要参数,而有些层不需要参数.CONV/FC层不仅仅对于输入进行激活,同时需要将权重和偏置作用在输入上.而RELU/POOL只是一个固定的函数,并没有参数.
总结:卷积神经网络就是一系列层组成,将输入图像体积转换为输出体积(体积表面了维度)
- 卷积神经网路包括完全不同的层(e.g. CONV/FC/RELU/POOl)
- 每一层通过一个可微的函数将3D volume的输入转换为3D volume的输出
- 有些层需要参数,有些不需要(e.g. CONV/FC 需要, RELU/POOlL不需要)
- 有些层需要额外的超参数,有些不需要(e.g. CONV/FC/POOL需要,RELU不需要)
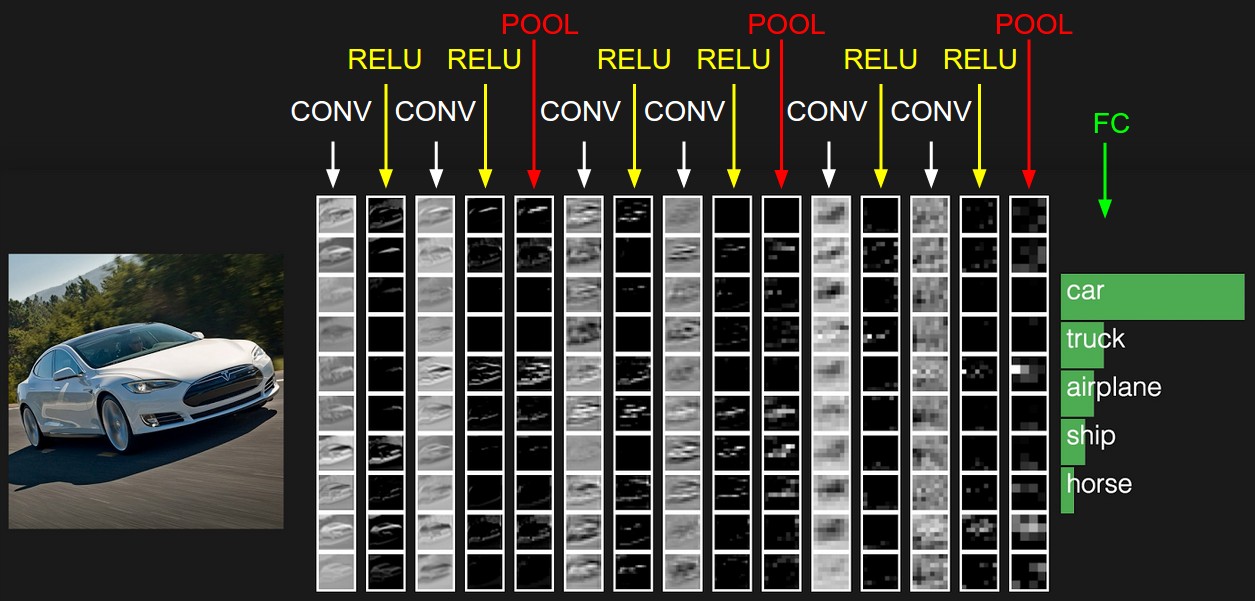
因为无法很难画出3D的部分,所以这里每一层只展示了深度部分的一片.最后给出了得分最高的五个标签.这里展示的是一个很小的 VGG网络.查看详细展示
卷积层
卷积层是卷积神经网络的核心部分,并且涉及了大量的计算.卷积层使用过滤器对于原图像进行卷积,过滤器每次只能针对整副图像的一部分进行计算,所以我们需要移动过滤器,遍历整个图像.这里过滤器的大小又叫做神经元的接收域.
Example 1:假设输入为[32$\times$32$\times$3],过滤器大小为5$\times$5,那么卷积层中的某个神经元需要的参数为5$\times$5$\times$3 + 1=76.为什么需要这么多的参数呢?针对颜色通道R,当前过滤器对应的局部区域的点是5$\times$5=25个,有三个通道,所有总的参数为75,另外再加一个偏置项,所有一个神经元总共需要76个参数.注意这里的深度为3,这是因为输入的深度是3.
Example 2:假设输入为[16$\times$16$\times$20],过滤器大小为3$\times$3,那么卷积层中每个神经元都需要3*3*20 + 1=180个参数.

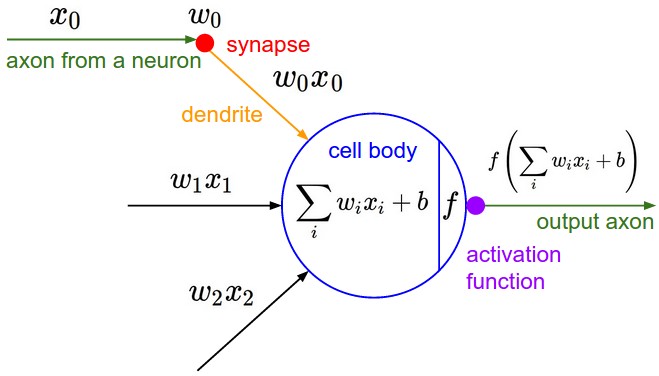
第一张图展示了卷积层,可以看到一个神经元连接了原图像的局部区域,但是连接了所有的深度(这是是三个颜色通道).这里展示了五个神经元,这五个神经元都连接到了图像的同一个局域上.第二张图展示了神经元的计算.
Spatial arrangement 前面我们仅仅讨论了卷积层中的每个神经元如何连接到前一层,我们还没有讨论在卷积层的输出中有多少个神经元.深度,步长,0值填充这些超参数控制着卷积层的输出的大小
- 卷积层输出的深度等于过滤器的数量,而每个过滤器就是去寻找输入到卷积层数据的不同之处.如果输入是原始图像,那么过滤器就是去寻找不同方向的边,颜色等.
- 步长是过滤器移动的长度,一般常用的是1和2
- 0值填充就是在卷积层的输入的边界上填充0值,使用0值填充使得我们能够控制经过卷积层之后的空间大小.
下面的公式可以用来计算卷积层输出的空间大小其中W(输入数据的大小),F(卷积层神经元的接收域大小),S(步长),P(零值填充的宽度).例如输入为7$\times$7,过滤器为3$\times$3,步长为1,不填充,则得出输出为5$\times$5.当步长变为2时,那么输出变为3$\times$3.

这里的输入只有一个x轴,输入为[1,2,-1,1,-3],过滤器大小为3,采用零值填充.所以W=5,F=3,P=1.图片最右侧是过滤器的权重,偏置为0.左图:步长为1,最后得到的输出的尺寸为5;右图:步长为2,最后得到的输出尺寸为3.所有黄色的神经元共享相同的参数
Use of zero-padding.当步长为1(即S=1),设置$P=(F-1)/2$,这样卷积层的输入跟输出将会有相同大小的空间.
Constraints on strides.